Categories for Greedy Bastards

Mar 5, 2016     

Magnus Larsson - "Downtown Vancouver Sunset"

I’ve really like the idea of Categories. They boil down one of the most essential aspects of programming - “composition” - into a concrete interface, and with their laws, give rise to logically intuitive behaviour. Categories start out extremely simply, with only two laws, and two operations, but the subject quickly becomes highly theoretical through many ideas about sub-categories, transformations between categories, isomorphic behaviors, etc. Still, just using the basics is very satisfying!

While categories may be intellectually stimulating, there was a question asked recently that I thought I would be able to easily answer, but the more I thought about it, the more I was stumped…

“How can a Category instance in my program save me from writing at least a little code?”

Index

What Are Categories?

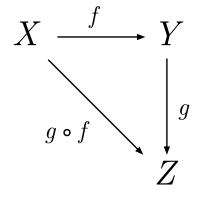
From “All Concepts are Kan Extensions (PDF)”:

When Samuel Eilenberg and Saunders MacLane first introduced the concept of a category in 1942, some mathematicians derided it as “general abstract nonsense” [7]. Categories seemed so theoretical that many doubted they would lend new insights in any field. Now, however, many category theorists view the “general abstract nonsense” phrase as a challenge, and have even co-opted the term for their own uses. They have demonstrated the tremendous power of and universal insights provided by category theory.

Category theory offers “a bird’s eye view of mathematics. From high in the sky, details become invisible, but you can see patterns that were impossible to detect from ground level” [5]. Category theory provides a mechanism to describe similarities within and between different branches of mathematics. Advances or constructions in one branch can be translated into other branches. Category theory focuses on the abstract structure of objects rather than on the elements of those objects.

Examples from Programming

Theory aside, Category could be considered an interface, or as in Haskell, a type-class:

class Category cat where
  id  :: cat a a
  (.) :: cat b c -> cat a b -> cat a c

Implementations provide identity, and composition, as well as satisfying the following laws:

  • Associativity: (f . g) . h = f . (g . h)
  • Left Unit: id . f = f
  • Right Unit: f . id = f

Some examples of categories in Haskell include:

  • Functions!
  • Kleisli - Composition of Monadic Binds
  • Arrows
  • Categories!
  • Unit - Just one thing
  • Void - Nothing
  • POSet
  • Diagrams

Why are categories cool?

If you can think of a hypothetical way to solve a problem as a set of abstract compositions of sub-solutions… Then you’ve basically solved it in some kind of category. I don’t know about you, but that’s almost always how I start to tackle the solution of most programming problems. For example, I wrote a simple text-tabulation program a while ago.

While this was before I’d really thought about categories, I was actually using category-composition operators (specialized to functions) just because they worked left-to-right and looked kinda cool!

You could essentially define the business-logic of my program as follows:

tabulate  = getLines
        >>> splitRows
        >>> indexedLengths
        >>> lengthEncodedRectangular rectangle
        >>> stripTrailingSpace
        >>> joinRows
        >>> joinLines

rectangle = longestLine
        >>> clean
        >>> columnize
        >>> indexedLengths
        >>> justified
        >>> joinRows

Now, I was already working with functions and lists, but if I started with this top-down expression of my function, and left the bodies of the implementations of these sub-solutions undefined, then had I asked for the types of tabulate and rectangle I would have seen:

[*Main] λ :i tabulate
tabulate :: Category cat => cat a c

[*Main] λ :i rectangle
rectangle :: Category cat => cat a c

Leaving me free, not just to decide my implementation, but also to decide my implementation’s categorical context…. Pretty rad!

The Code Objection…

So I was sold, I had a shiny new toy, and it was easy to use, and sounded super-impressive, so I talked about it quite a lot. It was during a discussion about just-what categories were that the question came up:

How can a Category instance in my program save me from writing at least a little code?

I started to respond confidently…

Well for any typeclass, the methods allow you to write in an abstract fashion with only a constraint referring to that class, giving you the oportunity for code reuse, etc, etc…

Then I was asked to give an example where that saved code in the case of Category.

Ah well, since you have id and compose then you can use these to… er… make a generic composition function like… um… compose three things… in um, like reverse order or something… hmm wait, that doesn’t sound like something very many people would want to do… nor does it really save any code since you have to reference the things you’re composing anyway… ah… Good question!

Yep. Stumped.

Also, even when you had a category, what did categorical composition ever really give you over using the composition operator specific to the category you were working with concretely… Like why, besides the cool factor, would you ever choose category composition over regular function composition?

The Code Objection Rebuttal - Mutation

So it came to me some time later, that the answer is… You wouldn’t!

If you’re writing a piece of code, then you won’t ever get to the end result in less lines by using Category. You can always do it with the specific composition operations faster, and more clearly implying your implementation and intent. Yes it is true. In the case of the construction of an end-goal program from green-fields from start to finish…

But… Programming involves more than just construction.

If you have to change your design, or refactor your implementations, especially multiple times, and in interesting ways involving new contexts, then you are no longer performing construction. You’re mutating your program. And THIS is where Category can begin to save you not only code, but stress too!

If you compose with Category then the code of your compositional pipelines (if the sub-solution decomposition is stable) can stay the same. It won’t have to change as you make radically different implications about the context your problem is solved in. You can go from a pure solution, to a stateful solution, to a monadic, or even highly abstract solution, all while leaving your expression of the decomposition of the problem alone. Not only that, but if you only switch to coherent instances of Category then as you mutate your implementation, your composition will always be sound.

You can take a load off your shoulders and relax.

Example: Refactoring Business Logic

Last week the big boss came over to you, the star developer, to solve a big business problem.

Boss: We need sales figures… Our partners have some horrible Excel reports that contain all kinds of useless stuff, but the figures are in those reports somewhere. We don’t have time to do this by hand every week, so we want you to make a program to pull out those figures!

You: No worries boss.

What a great problem! It’s not especially cool or anything, but it has some nice properties. It’s just a process, so you can use your favorite functional language. It’s just a data-transformation problem, so your functions can be pure! Just a little IO required to pull in the data, then spit out the results. It sounds nice and easy, but should be a little brain-teaser and can let you tinker for a while before you have to go back to configuring Drupal oh god.

Classically

Woo. Done ~

excellerator :: Excel -> [Int]
excellerator e = e & parse & explode & filter & locate & extract & format

parse   = ...
explode = ...
filter  = ...
locate  = ...
extract = ...
format  = ...

You: Here you go boss. All finished. Enjoy those sales figures!

Boss: Oh I will… I will…

Mr. Burns

You relax and bask in the glory for a couple of days, then just as you’re ready to get back to that other problem involving configuration that you’ve been avoiding…

Legal: Hey good work on that sales-figures process, but we need you to make a change.

You: Oh?

Legal: Yeah… We know your filtration process is working, but we need you to log the removed items so that we can prove we’re not misrepresenting the partner… They’re being a dick.

You: Makes sense… But now I have to change my beautiful program…

Legal: We don’t care about that.

You: Hmm… Okay. I’ll do it. Get back to you soon…

Damn, the original code was just so elegant. But now you have to do what? Logging? Right in the middle of it all? Ah jeez…

But, last week you read about monads… Hmm, and you read about the Writer monad. What if instead of normal function composition you used monadic composition. And then you could just lift your existing functions into the monadic context, and leave them alone, and you could change the filter function to also perform logging on the removed rows. Wow this is gonna be great!

excellerator :: Excel -> Writer [RemovedID] [Int]
excellerator = parse >=> explode >=> filter >=> locate >=> extract >=> format

parse   = fmap $ ...
explode = fmap $ ...
filter  = ... -- Updated code to perform logging of row removal
locate  = fmap $ ...
extract = fmap $ ...
format  = fmap $ ...

Not bad.

Categorically

Now we come to the punch-line.

What if the excellerator changes could have been just the signature?

Purely:

excellerator :: Excel -> [Int]
excellerator = parse >>> explode >>> filter >>> locate >>> extract >>> format

After the logging change:

excellerator :: Kleisli (Writer RemovedID) Excel [Int]
excellerator = parse >>> explode >>> filter >>> locate >>> extract >>> format

Notice how the implementation of excellerator did not change.

Of course, your sub-solution implementations will still have to be updated, but you would have had to do that anyway. And now you also get the nice bonus that you can change to other Categories too, IO, State, whatever!

So there you go. Code saved.

Complications

Funnily enough, when I presented this talk to the same group who had raised the inspirational question -

“How can a Category instance in my program save me from writing at least a little code?”

… they asked another -

“does this form of abstraction provide much over a scoped definition of composition?”

This is also a good one, but at least I have something of an answer ready in response.

I believe that, scoping and redefinition boilerplate aside, the advantage that using category instances gives you over simply redefining a custom composition operator is the fact that your composition is coherent. This has to be the case because of the very fact that you are using a Category where composition is meaningful and correct by definition.

Links

Apendix

A Different Working Example

Here is an example of a what a similar refactoring would have looked like if Category instances were used to express the business pipeline.

Imports:

{-# LANGUAGE RankNTypes #-}
{-# LANGUAGE KindSignatures #-}

import Control.Category    ((>>>), Category())
import Control.Arrow       (Kleisli(..))
import Control.Monad.State (runState, modify, State)

Pure Implementation:

main = print (pipeline 1)

pipeline :: Int -> String
pipeline = a >>> b >>> c
  where
  a = (+1)
  b = (+2)
  c = show

Here - IO:

main = (runKleisli pipeline' 2) >>= print

pipeline :: Kleisli IO Int String
pipeline = a >>> b >>> c
  where
  a = Kleisli $ return . (+1)
  b = Kleisli $ \x -> print x >> return (x + 2)
  c = Kleisli $ return . show

Here - State:

main = print (runState (runKleisli pipeline'' 3) 0)

pipeline :: Kleisli (State Int) Int String
pipeline = a >>> b >>> c
  where
  a = tally (+1)
  b = tally (+2)
  c = tally show
  tally f = Kleisli $ \x -> modify (+x) >> return (f x)